Table of Contents
Programmazione strutturata
Introduzione
Quando si affronta la programmazione si devono indicare al computer delle istruzioni da eseguire. Se il computer potesse comprendere il linguaggio naturale, sarebbe facile chiedere:
- di eseguire un'istruzione condizionale: se questo è vero, fai una cosa, altrimenti fai quest'altra cosa;
- di eseguire un'istruzione iterativa: ripeti questo per 100 volte;
- di eseguire una sequenza di istruzioni: fai prima questo, poi fai questo e poi quest'altro.
Si tratta di istruzioni per noi molto semplici da comprendere, ma che devono essere espresse in modo da poter essere comprese dal computer. Ognuna delle precedenti istruzioni è un esempio di: una condizione, un'iterazione e una sequenza.
Teorema Böhm-Jacopini
Questo teorema afferma che qualsiasi algoritmo può essere descritto utilizzando solo tre tipi di strutture: la sequenziale, la condizionale e l'iterativa.
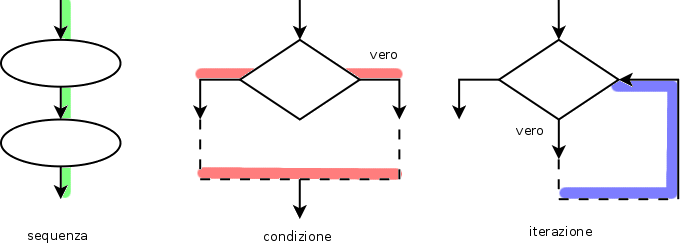
Gli esempi appena visti erano proprio di queste strutture:
I programmi che seguiranno sono privi di altre funzioni oltre al main() per mettere in evidenza solo queste tre strutture. Al loro fianco sarà presente un diagramma di flusso che usa gli stessi colori per mettere in evidenza le tre strutture.
Le tre strutture possono anche essere combinate insieme tra di loro: si può inserire una struttura sequenziale all'interno di una condizionale(Figura 1), oppure una struttura condizionale dentro una struttura iterativa (Figura 2).

Traduzione in C++
Poiché queste tre strutture sono indispensabili per descrivere gli algoritmi, ogni linguaggio di programmazione consente di tradurle come istruzioni. Nei prossimi esempi si vedrà che
- La struttura sequenziale si traduce in C++ usando una coppia di parentesi graffe
{
...
}
- La struttura condizionale si traduce in C++ usando un'istruzione if eventualmente seguita da else
if ( ... )
...
else ...
- La struttura iterativa precondizionale in C++ si può tradurre in due modi diversi, tra loro equivalenti, usando while() oppure for():
while( ... ) ...
for( ...; ...; ...) ...
Struttura sequenziale
Un programma può eseguire una lista sequenziale di istruzioni
- Esempio che calcola l'area di un cerchio
- chiedere in input un valore per il raggio
- calcola l'area di un cerchio (formula…)
- visualizzare in output l'area
| var. di input | tipo | var. di output | tipo | var. di lavoro | tipo |
|---|---|---|---|---|---|
| raggio | num. virgola | area | num. virgola | area | num. virgola |
La struttura sequenziale si traduce in C++ usando una coppia di parentesi graffe
{
...
}
- 31.cpp
// Questo programma è stato scritto da Fabio #include <iostream> int main() { std::cout << "Inserisci il valore del raggio del cerchio: " << std::endl; float raggio; std::cin >> raggio; float area = raggio*raggio*3.14; std::cout << "L'area del cerchio vale: " << area << std::endl; return 0; }
Struttura condizionale
Un programma può eseguire istruzioni diverse in base al verificarsi di una condizione

- Esempio che visualizza la maggiore età
- chiedere in input il valore dell'anno di nascita
- calcolare l'età attuale
- se età < 18
- allora visualizzare in output: sei minorenne
- altrimenti visualizzare in output: sei maggiorenne
| costanti | valore | var. di input | tipo | var. di output | tipo | var. di lavoro | tipo |
|---|---|---|---|---|---|---|---|
| annoAttuale | 2012 | annoNascita | intero | - | - | - | - |
La struttura condizionale si traduce in C++ indicando la condizione dentro il rombo dentro un'istruzione if che contiene tra parentesi la condizione da verificare. Dopo si scrive l'istruzione (o le istruzioni) da eseguire nel caso “vero”. Poi, nell'eventualità che vi siano istruzioni nel caso “falso”, si scrive anche else e le sue eventuali istruzioni.
if ( ... )
...
else ...
- 32.cpp
// Questo programma è stato scritto da Fabio #include <iostream> int main() { const int annoAttuale=2012; std::cout << "Per favore scrivi l'anno di nascita: "; int annoNascita; std::cin >> annoNascita; if ( annoAttuale-annoNascita < 18 ) std::cout << "Minorenne." << std::endl; else std::cout << "Maggiorenne." << std::endl; return 0; }
Che differenza c'è tra questi due esempi di istruzione if? Perché vengono entrambi compilati senza segnalare errore?
if ( eta == 18 )
if ( eta = 18 )
Operatori logici
L'algebra di Bool (booleana) è un'algebra nata per definire la logica delle proposizioni, dove si studia lo stato (il valore) di verità delle proposizioni. Una proposizione può essere vera oppure falsa.
ATTENZIONE: non confondere in italiano il termine proposizione con preposizione, che ha un altro significato…
Esempio di proposizione (con valore tra parentesi):
- P = “il quadrato ha 4 lati” (vero)
- Q = “il tuo cane miagola” (falso)
In tale algebra esistono diversi operatori (detti operatori booleani oppure connettivi logici) che possono essere applicati ad una o più proposizioni.
- AND (detto congiunzione)
- OR (detto disgiunzione)
- NOT (detto negazione)
- altri meno famosi come: NAND, NOR, XOR,…
Esempio di NOT
Applicando l'operatore NOT alle due precedenti proposizioni il loro valore di verità diventa l'opposto:
- NOT P = “il quadrato NON ha 4 lati” (falso)
- NOT Q = “il tuo cane NON miagola” (vero)
Esempio di AND
Applicando l'operatore AND, si ottiene una nuova proposizione il cui valore di verità dipende dalla verità di entrambe le proposizioni di partenza (è vera solo se sono entrambe vere)
- P AND Q = “il quadrato ha 4 lati” E “il tuo cane miagola” (falso)
Esempio di OR
Applicando l'operatore OR, si ottiene una nuova proposizione il cui valore di verità dipende dalla verità di entrambe le proposizioni di partenza (è vera se almeno una delle due è vera):
- P OR Q = “il quadrato ha 4 lati” OPPURE “il tuo cane miagola” (vero)
La tabella di verità
Per ogni operatore booleano (AND, OR, NOT, ecc.) si può costruire una tabella che aiuta a descriverlo. Nella seguente tabella sono messe a confronto gli operatori AND e OR. Le prime due colonne sono due proposizioni su cui applicare tali operatori.
| P | Q | P AND Q | P OR Q |
|---|---|---|---|
| V | V | V | V |
| V | F | F | V |
| F | V | F | V |
| F | F | F | F |
La tabella di verità del NOT è più semplice:
| P | NOT P |
|---|---|
| V | F |
| F | V |
Il calcolo automatico
Dopo circa un secolo dalla sua ideazione, l'algebra di George Boole ha trovato applicazione anche nell'elaboratore. Poiché l'elaboratore utilizza il sistema di numerazione in base 2, al valore “vero”(true) viene fatto corrispondere il valore 1 mentre al “falso”(false) lo 0. Più in generale, si può dire che qualsiasi valore diverso da 0 è considerato “vero”, infatti, in quasi tutti i linguaggi di programmazione il numero intero ZERO viene interpretato come “falso”.
Il programmatore può scrivere espressioni hanno un risultato numerico, come x=33*4; o espressioni che hanno un risultato “vero” o “falso”, come x>0.
Alle espressioni di confronto, come a<b, possono essere applicati i precedenti operatori logici. Il calcolo automatico di queste espressioni (come a<b) permette al programma di eseguire un'istruzione oppure un'altra a seconda se l'espressione venga valutata “vera” oppure “falsa”.
Nelle istruzioni di scelta condizionata sarebbe opportuno usare solo il secondo tipo, ma questa non è una regola fissa. Quando vengono usate le espressioni che producono un risultato numerico, il numero viene automaticamente convertito in “falso” o “vero”. Se vale zero è “falso”, se è diverso da zero è “vero”.
Traduzione in C++
Nel linguaggio C++ gli operatori logici AND, OR e NOT vengono tradotti con i seguenti simboli:
| operatore | simbolo |
|---|---|
| AND | && |
| OR | || |
| NOT | ! |
Per l'ordine di precedenza vedereoperazioni_su_int

- Esempio di algoritmo che prevede la presenza di nebbia quando si verificano le seguenti condizioni: umidità relativa compresa tra il 85% e il 90%.
- chiedere in input il valore di umidità relativa (massimo 100)
- se umidita > 85 && umidita < 90
- allora visualizzare in output “previsione di nebbia”
- altrimenti visualizzare in output “non si prevede nebbia”
- 32b.cpp
// Questo programma è stato scritto da Fabio // visualizza le previsioni per la nebbia // fornendo la percentuale di umidita' relativa. // Domanda: cosa accade se inserisco un valore negativo? #include <iostream> int main() { int umidita; const int umiditaMin=85; const int umiditaMax=90; std::cout << "Per favore scrivi il valore di umidita' relativa, come intero da 0 a 100." << std::endl; std::cin >> umidita ; if ( umidita > umiditaMin && umidita < umiditaMax ) // attenzione alla precedenza degli operatori... std::cout << " si prevede nebbia " << std::endl; else std::cout << " non si prevede nebbia " << std::endl; return 0; }
Struttura condizionale annidata
- Esempio che visualizza il minimo di tre numeri
- chiedere in input 3 valori numerici interi (primo,secondo,terzo)
- se primo < secondo
- allora: Se primo < terzo
- allora visualizzare in output: primo
- altrimenti visualizzare in output: terzo
- altrimenti: Se secondo < terzo
- allora visualizzare in output: secondo
- altrimenti visualizzare in output: terzo
| var. di input | tipo | var. di output | tipo | var. di lavoro | tipo |
|---|---|---|---|---|---|
| primo | num. intero | primo | num. intero | - | - |
| secondo | num. intero | secondo | num. intero | - | - |
| terzo | num. intero | terzo | num. intero | - | - |
- 33.cpp
// Questo programma è stato scritto da Fabio // visualizza il minimo di tre numeri #include <iostream> int main() { int primo,secondo,terzo; std::cout << "Inserire tre numeri interi separandoli con 'invio' " << std::endl; std::cin >> primo >> secondo >> terzo ; if ( primo < secondo ) if ( primo < terzo) std::cout << "primo: " << primo << std::endl; else std::cout << "terzo: " << terzo << std::endl; else if ( secondo < terzo ) std::cout << "secondo: " << secondo << std::endl; else std::cout << "terzo: " << terzo << std::endl; return 0; }
Condizione con operatore logico AND
- 34.cpp
// Questo programma è stato scritto da Fabio // visualizza il minimo di tre numeri // utilizzando gli operatori logici in alternativa alle condizioni annidate #include <iostream> int main() { int primo,secondo,terzo; std::cout << "Inserire tre interi separati da invio" << std::endl; std::cin >> primo >> secondo >> terzo ; if ( primo < secondo && primo < terzo ) std::cout << primo ; else if ( secondo < terzo ) std::cout << secondo ; std::cout << terzo ; return 0; }
TO DO
deve essere fatto un esercizio con if if else per spiegare il caso dell'ambiguita' dell'else e di come si risolve tale ambiguità
Esercizi:
- esercizio: chiedere due numeri e visualizzarli in ordine inverso
- esercizio: chiedere due numeri, senza un ordine, visualizzare uno dei tre messaggi: sono ordinati, sono disordinati, sono uguali.
Struttura iterativa
La struttura iterativa può essere studiata come composta da diversi elementi (che possono anche coincidere tra loro):
- un'elenco di istruzioni da ripetere
- un'eventuale variabile contatore (per numerare e contare quante sono le ripetizioni effettuate)
- un'eventuale variabile totalizzatore (per accumulare l'eventuale risultato di tutte le operazioni ripetute)
- la valutazione di un'espressione logica di uscita o condizione di uscita (per terminare in qualche modo la ripetizione)
- un'eventuale istruzione che modifica la variabile contenuta nella condizione di uscita (ad esempio l'incremento del contatore…)
A seconda della posizione occupata dalla condizione di uscita all'interno della ripetizione, la struttura iterativa può essere di due tipi:
- precondizionale
- postcondizionale
Nel tipo precondizionale la condizione è prima delle istruzioni da ripetere. Nel tipo precondizionale, quando la condizione di uscita non è verificata, le istruzioni da ripetere non vengono mai eseguite, mentre nella postcondizionale la ripetizione viene eseguita sempre almeno una volta. In entrambi i casi si esce dal ciclo di ripetizione quando la condizione diventa falsa.
Struttura iterativa postcondizionale
Anche se esiste, si possono scrivere programmi senza usarla, quindi per ora viene omessa…
Struttura iterativa precondizionale
Precondizionale significa che la condizione di uscita precede la ripetizione, quindi, in questo caso, potrebbe accadere che, se la condizione non è verificata, la ripetizione non sia mai eseguita
La struttura iterativa precondizionale in C++ si può realizzare in due modi di scrivere diversi, tra loro equivalenti:
- while()
- La condizione di uscita del rombo deve essere indicata tra le parentesi di while. L'eventuale inizializzazione del contatore va indicata subito prima di while. Le istruzioni da ripetere, così come l'istruzione che modifica il valore del contatore, vanno indicate subito dopo while, se necessario si possono aggiungere due parentesi graffe per racchiudere le istruzioni da ripetere.
//eventuale inizializzazione contatore... while( ... ) ...
- for(;;)
- L'istruzione for contiene tra parentesi tre elementi separati dal punto e virgola (;), che sono i seguenti: l'eventuale inizializzazione del contatore, la condizione di uscita e l'eventuale istruzione che modifica il Contatore. Dopo si indica l'istruzione (o le istruzioni) da ripetere, eventualmente tra parentesi graffe.
for( ...; ...; ...) ...
Il seguente esempio è stato tradotto in due diversi programmi, tra loro equivalenti, per capire come si usa while() e come si usa for(;;). Il programmatore è libero di scegliere le due forme perché sono equivalenti.
- Esempio che visualizza la tabellina del numero inserito
- ripetere la seguente operazione per un indice (i) che va da 1 a 10
- visualizzare in output il risultato dell'espressione: numero*i
| var. di input | tipo | var. di output | tipo | var. di lavoro | tipo |
|---|---|---|---|---|---|
| numero | num. intero | - | - | i | num. intero |
- 35.cpp
// Questo programma è stato scritto da Fabio // iterazione realizzata con while #include <iostream> int main() { int numero; std::cout << "Inserisci un numero intero da 1 a 10" << std::endl; std::cin >> numero ; int i=1; // inizializzazione del contatore while ( i <= 10 ) // condizione di uscita { std::cout << numero * i << ' ' ; i++; // incremento del contatore } std::cout << std::endl; return 0; }
- 35b.cpp
// Questo programma è stato scritto da Fabio // iterazione realizzata con for #include <iostream> int main() { int numero; std::cout << "Inserisci un numero intero da 1 a 10" << std::endl; std::cin >> numero ; for ( int i=1; i<=10; i++) // inizializzazione, condizione ed incremento... std::cout << numero*i << ' ' ; std::cout<< std::endl; return 0; }
- inizializzare totale a zero
- ripetere la seguente operazione per i che va da 1 a 5
- chiedere in input numero
- incrementare totale con numero
- visualizzare totale
- 36.cpp
// Questo programma è stato scritto da Fabio // iterazione realizzata con while #include <iostream> int main() { int totale=0, i=1, numero; //inizializzazione di contatore e totalizzatore while ( i <= 5 ) { std::cout << "inserire un numero " ; std::cin >> numero; totale = totale + numero; i = i + 1; } std::cout << totale << std::endl; return 0; }
- 36b.cpp
// Questo programma è stato scritto da Fabio // iterazione realizzata con for #include <iostream> int main() { int numero,totale=0; for ( int i=1; i<=5; i++) { std::cout << "Inserisci numero" << i<< std::endl; std::cin >> numero ; totale = totale + numero; } std::cout << totale << std::endl; return 0; }
Struttura iterativa annidata
Scrivere un programma che visualizzi tutte le tabelline pitagoriche dall'uno al dieci.

- 37.cpp
// Questo programma è stato scritto da Fabio // visualizza la tabellina dell'uno sulla prima riga // la tabellina del due sulla seconda riga, e cosi via. #include <iostream> #include <iomanip> int main() { int i=1; while ( i<=10 ) { int j=1; while ( j<=10 ) { std::cout << std::setw(3) << j*i << ' ' ; j=j+1; } i=i+1; } std::cout << std::endl; return 0; }
- 37b.cpp
// Questo programma è stato scritto da Fabio // visualizza la tabellina dell'uno sulla primaa riga // la tabellina del due sulla seconda riga, e cosi via. #include <iostream> #include <iomanip> int main() { for ( int i=1; i<=10; i++) { for ( int j=1; j<=10; j++) std::cout << std::setw(3) << j*i << ' ' ; } std::cout << std::endl; return 0; }
Struttura iterativa all'interno di struttura condizionale
- Ad esempio, inserendo 5 e 9 viene visualizzato 6,7,8, mentre inserendo 9 e 5 viene visualizzato 5.
- provaacontare.cpp
#include <iostream> int main() { int num1,num2; std::cout << "Per favore inserire due numeri interi " << std::endl; std::cin >> num1 >> num2 ; if (num1<num2) { int i=num1+1; while (i<num2) { std::cout << i << ", "; i=i+1; } } else std::cout << num2 << std::endl; return 0; }
Struttura condizionale all'interno di struttura iterativa
- Esempio in cui si inseriscono due numeri interi e si visualizzano tutti i numeri intermedi ad eccezione del numero 7. (inserendo 3 e 8 si visualizza: 3,4,5,6,8)
- SENZA SOLUZIONE
Numero di ripetizioni sconosciuto
fare la somma di tutti i numeri inseriti fino a che si inserisce 0 per visualizzare il totale 
- 37b.cpp
// Questo programma è stato scritto da Fabio // somma dei numeri senza dover sapere quanti sono #include <iostream> int main() { int totale=0, numero=-1; // inizializzazioni while(numero != 0) { std::cout << "inserire numero " << std::endl; std::cin >> numero ; totale = totale + numero; } std::cout << numero << std::endl; }
Cenni alla ricorsione
Premessa
Un programma che ripete più volte la stessa operazione, in teoria, può essere scritto secondo due approcci:
- l'iterazione (precedentemente vista)
- la ricorsione
Esempio del fattoriale di un intero N
Chi volesse utilizzare l'approccio della iterazione per spiegare come si calcola il fattoriale, potrebbe usare le seguenti parole:
- ripetere per i da 1 a N
- moltiplicare tra loro tutte i valori di i
Chi volesse utilizzare l'approccio della ricorsione, invece, potrebbe dire:
- moltiplicare N * (N-1)
- moltiplicare il risultato precedente per (N-2)
- moltiplicare il risultato precedente per (N-3)
- … e così via…
- fino a 1
Nell'approccio ricorsivo, le parole “e così via” descrivono l'espressione della soluzione in termini di uso quotidiano. Quindi, sebbene, in teoria, ogni problema possa essere risolto usando entrambi gli approcci, vi sono alcuni problemi che si prestano ad essere risolti più facilmente in un modo piuttosto che nell'altro.
Condizioni
Per risolvere un problema con una ricorsione è necessario:
- esprimere la soluzione del passo generico i nei termini del passo precedente (i-1), ad esempio:
fattoriale(i) = i*fattoriale(i-1); // esprime il problema nei termini di se stesso
- esprimere una condizione di terminazione, ad esempio:
fattoriale(0) = 1;
- 41.cpp
// calcolo del fattoriale #include <iostream> int main() { int numero, fattoriale=1; std::cout << "Inserire un numero intero positivo: " << std::endl; std::cin >> numero; for (int i=1; i<=numero; i++) fattoriale = numero*fattoriale; std::cout << "Il fattoriale di " << numero << " vale " << fattoriale << std::endl; return 0; }
Verifica
L'utente inserisce un numero intero compreso tra 1 e 10. L'elaboratore visualizza tutti i numeri compresi tra 1 e 10 ad eccezione di quello inserito dall'utente. Se l'utente inserisce 4, il computer visualizza 1,2,3,5,6,7,8,9,10